Randomness of bits with LCGs
In addition to the rather serious problem of pairs or triples (etc) of numbers
"falling in the planes", random numbers produced by
LCGs such as java.lang.Random have another serious drawback: in the
numbers produced, randomness depends on bit position. That is,
in the numbers produced by (say) Random.nextInt(), the lower bits will be
less random than the upper bits.
As a graphic example of the problem, let's suppose we create a 256x256 pixel square,
with each pixel coloured either black or white. We'll decide on the colour of the pixel
depending on the bottom bit of successive values returned by Random.nextInt().
So the program would look something as follows:
Random r = new Random();
BufferedImage bimg = new BufferedImage(256, 256,
BufferedImage.TYPE_BYTE_BINARY);
int w = bimg.getWidth();
for (int y = 0; y < bimg.getHeight(); y++) {
for (int x = 0; x < w; x++) {
int bit = r.nextInt() & 1;
bimg.setRGB(x, y, (bit == 0) ? 0 : 0xffffff);
}
}
So when we run this, we might reasonably expect to see our square filled with "snow" with
no discernible pattern. Well, Figure 1 shows what we actually get. We can clearly see long "stripes",
"checkerboards" and other patterns with much greater frequency and regularity than we would expect
by chance1. This happens because we are using the part of the integer which has the lowest degree
of randomness. It also has the lowest period.
We can improve on Figure 1 by taking higher bits. Figure 2 shows what happens
if we replace the line in bold with the following:
int b = (r.nextInt() >>> 2) & 1;
The result is better, but there are still some clear "spikes" where runs of the same value occur
again with much higher frequency than we'd expect.
Now of course, the implementers of java.lang.Random knew perfectly well about these
limitations. Even Figure 1 is actually better than it could have been. When we call
nextInt(), this method actually discards the very lower 16 bits of every number it
generates: the 32-bit integer that it returns us is actually the top 32 bits of
a 48-bit number generated internally. And if we want to generate a series of random bits,
then we whould ideally pull them from the part of that 48-bit number that is known to be
most random: namely, the topmost bit. And that's precisely what
Random.nextBoolean() does. Figure 3 shows the resulting plot if we use
Random.nextBoolean().
|

Figure 1: 256x256 of the low bit of successive calls to Random.nextInt().
|

Figure 2: 256x256 of the third-lowest bit of successive calls to Random.nextInt().
|
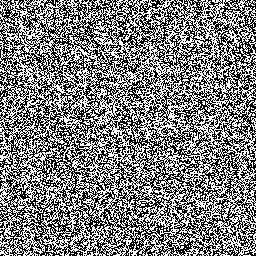
Figure 3: 256x256 of successive bits returned by Random.nextBoolean().
|
Calling the appropriate method
The above example is a reminder that when working with java.lang.Random and its subclasses,
we should use the specific method that provides the function we require, if available.
(For more information, see: java.lang.Random methods.)
In particular:
- always use the appropriate method for retrieving a random number
from java.lang.Random:
- to generate a random bit, use nextBoolean() rather than going
from the results of nextInte() etc;
- to generate a random byte, or a random number within a particular
range, use the version of nextInt() that takes an upper bound;
- avoid the idiom nextInt() % n— if n is a power of 2, then we're effectively
taking bits off the bottom. (You should actually avoid this idiom anyway, as for non-powers of 2, it
actually biases the results.)
- essentially the same point expressed another way: use all the bits of the number you are given!
If you call nextInt() and then only use the bottom few bits, you're actually discarding the
part of the number that is most random!
- as a specific case of the previous point, avoid testing for equality with a power of 2 on the lower bits of a random number,
where you are in effect testing for a single bit out of one of the lower bits:
if ((nextInt() & 0xff) == 8) {
...
}
In any application, the behaviour of java.lang.Random (and LCGs in general) described here
is liable to introduce subtle patterns into your "random" data. Clearly, this makes the class unsuitable for
"serious" uses of random numbers such as Monte Carlo experiments, gambling applications, cryptography etc.
But even for fairly "casual" applications such as generating test data for an application, the
disparity in randomness across the bits of generated numbers can cause problems.
Improved random number generators in Java
Although java.lang.Random serves as a base class for random number generators, other
random number generators are available in the Java platform that address the
shortcomings that we have described. See the introduction to random numbers in Java
for a list of the different classes.
1. It's important to consider, of course, that what seem to us as unlikely
will occasionally happen "by pure chance". For example, consider a block of 8 pixels. With each
pixel having a perfect 0.5 probability of being set, than there is still a 1 in 256 chance that these
8 pixels will form some given pattern, such as a checkerboard. (And the chance of there being "a checkerboard
somewhere" is of course greater if we allow, say, either 0101 or 1010 to count.)
Similarly, taking 256x256=65536 pixels, by pure chance we would
expect on average to find one run of 16 pixels set to the same value. Although our technique for
spotting the patterns is informal here, it is clear in Figure 1 that
these patterns occur with far greater frequency and regularity than expected by chance.
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.