Bloom Filters: the false positive rate (ctd)
Running our simulation to measure the false
positive rate of Bloom filters under different configurations, Figure 1 shows how the
percentage varies as a function of size of the filter and number of hash codes.
In effect, the first value along the X axis represents a bit set size of 1 bit per item,
the second value (215) 2 bits per item, the third (216) 4 bits per
item etc1.
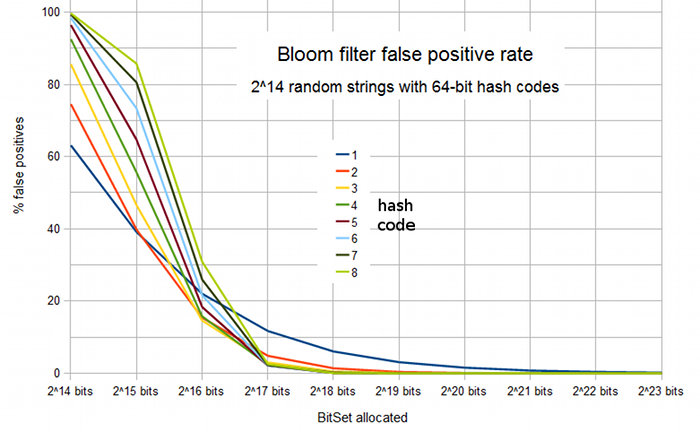
Figure 1: False positive rate of a Bloom filter representing a set of
214 strings, as a function of number of bits allocated to the
filter and the number of hash codes.
As intuitively expected, assigning only a very small number of bits per item
results in very high false positive rates. With one or two bits per item, adding
more hash codes is also of no benefit: it simply serves to "fill up" the bit
set more quickly and hence increases rather than decreases the false positive rate.
At 4 bits per item, adding more hash codes initially does improve the false positive rate,
up to an optimum value of 3 hash codes and a false positive rate of 14.6%.
Beyond this, we have gone past the "point of no return" where more hash codes
effectively fill the bit space too quickly.
With 8 bits per item, the optimum false positive rate (2.14%) occurs with
6 hash codes. However, as is often the case, there is a range of values where
we might argue that the benefit of adding an extra hash code rapidly diminishes.
Figure 2 shows more clearly how false positive rate varies as a function of
the number of hash codes, for Bloom filters with 8 bits and 16 bits per item.
After a clear benefit for the first 2 or 3 hash codes, the curve rapidly plateaus
in both cases.
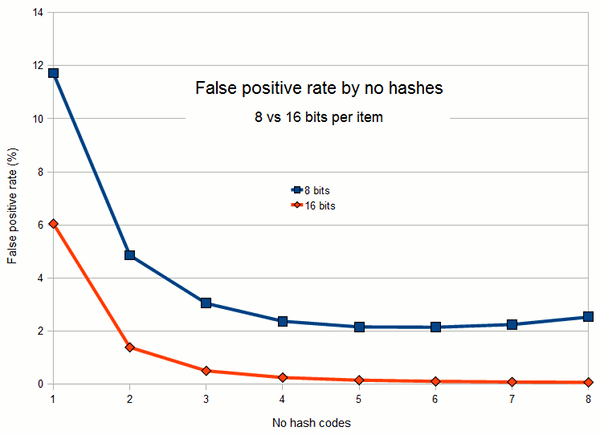
Figure 2: False positive rate by number of hash codes, showing the
increasingly diminishing returns of adding an extra hash code up to the
optimum value.
The information we have seen means that for many applications, reasonable
Bloom filter configurations will have between 4 and 16 bits per item and
between 2 and 4 hash codes. Table 1 below gives the actual false positive rates
observed2 in our experiment for values within these ranges:
| Hash codes | 4 bits/item | 8 bits/item | 16 bits/item |
|---|
| 2 | 15.4% | 4.8% | 1.4% |
| 3 | 14.6% | 3.0% | 0.49% |
| 4 | 15.8% | 2.4% | 0.24% |
Note that the mean bits per item does not actually need to be a power of 2:
intermediate values, giving intermediate false positive rates, are in principle possible.
1. Of course, this actually means that a size of 223, or 1024 bits
per item, is vastly unrealistic: our implementation is based on 64-bit hash codes,
so our purpose of using a Bloom filter is to improve on the 64 bits or so per item that
would ordinarily be required for a "normal" hash set that stored only the hash codes.
2. All of the percentages given are the mean of 10 runs of testing 1 million random
strings (so 10 million strings in total) as described in the previous section.
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.