Home
Collections intro
Lists
Maps
Sets
Which collection class?
Sorting
Hashing
Advanced
Video lecture: hash tables
Bloom filters
How the String hash function works (and implications for other hash functions)
In our introduction to hash codes, we mentioned the principal design aim of a generic hash code. By generic, we mean a hash code that will cope with fairly "random typical" input and distribute the corresponding hash codes fairly randomly over the range of integers (4 bytes in the case of Java). That way, whatever the size of our hash table, we assume that the keys will be distributed reasonably evenly among the buckets. For those that don't want to delve too deeply into the technical details, we gave some basic guidelines for writing a hash function.
On this page, we will delve a little more deeply into the technical details of hash codes. As an example, we'll look specifically at the hashCode() method used by the Java String class.
Randomness, mathematically speaking
There's actually quite a lot of overlap between the field of random number generators and the field of hash functions. For now, we will start by borrowing the concept of a randomness. We will say that a number (such as a hash code) is random if all its bits have an equal and independent chance of being either 0 or 1. Another general concept we'll borrow is that some initial randomness has to come from somewhere. A random number generator, is generally designed to take some unpredictable seed– such as the number of nanoseconds since the computer was switched on– as its initial source of randomness, and then from that generate a further (approximately) random sequence.
Where does randomness come from?Now let's get back to hashing the characters of a string and let's look at some typical character data. We'll consider generating a series of random strings, where each successive character has a particular change of being within a particular range:
|
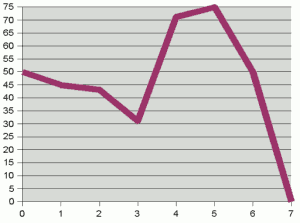
Plot of (bit number, probability of that bit being set) for an example character distribution |
This distribution of characters is essentially made up for illustration purposes. But the point is that any set of strings for a particular purpose will generally have some characteristic distribution. (There may well be interactions between successive characters too: for example in English, u is a relatively rare letter, but after a q becomes extremely likely as the next letter. We won't worry too much about this here.) Now, given this character distribution, we can calcualte the probability of each bit being set for a random character in a string. The graph above right shows this probability distribution.
It is clear from the graph that the bits of the characters are not randomly distributed. If they were, we'd expect to see a flat line at 50%. Instead, the first three or four bits "hover" around and below the 50% mark– i.e. are "more or less random"– but higher bits are heavily biased towards particular values. For a given character, there is a better than 70% chance that bit 4 will be set, and a 75% chance that bit 5 will be set. This lack of randomness happens almost by design– the ASCII standard was built with certain correspondences in mind, such as bit 5 being set to mark a lower case character.
So what can we do create more-or-less random hash codes? Well, we can take those bits that are more or less random (the low bits) and, as we build up the hash code, try and make them interact so that they "spread the randomness out" over the integer. On the next page we look in more detail at spreading the random bits in a hash function.
Written by Neil Coffey. Copyright © Javamex UK 2012. All rights reserved. If you have any feedback on the Java collections tutorials in this section or about the content of this site in general, please leave a message on the Javamex forum.