Math.exp() in Java: performance and approximations
The Math.exp() method, as mentioned in our overview of methods
provided by the java.util.Math class,
implements the so-called exponential function or ex.
This function
crops up in a number of applications. Like a number of mathematical
functions, it is one whose output is impossible to calculate exactly*. Instead,
it can only be calculated with a certain degree of precision, and when
calculating ex we must therefore decide how much precision
we require. The Math.exp() method makes this decision for you:
in line with the IEEE standard,
the method is obliged to give ex as
accurately as possible in double representation, but is implemented so
as basically to go to "just enough effort". This has two
consequences we should be aware of:
- the time required by Math.exp() actually varies slightly depending
on the input value;
- if we require less precision that theoretically allowed by a double,
we may be able to use our own, faster, approximation at the expense of this
loss of accuracy.
* Exception: as with any number raised to the power 0,
when x is 0, ex is of course equal to 1 precisely.
Time taken by Math.exp()
The implementation of Math.exp() relies firstly on the fact that ex
can be broken down as follows:
e x0 + x1 ≡
ex0 ex1
It secondly relies on the fact that because of the way floating point numbers are
represented, multiplying by a power of two can be done extremely quickly (it is effectively
an addition in the higher bits of the number).
The implementation thus breaks x down into x0 and x1 such
that ex0 is a power of 2 (which, if you do the math,
means that x0 is a whole number of multiples of the natural logarithm
of 2).
Then, it calculates
ex1 as accurately as necessary within the
constraints of a double. Finally, if the x0 component is non-zero,
this is multiplied into the final answer using the aforementioned "adding in the upper
bits" trick.
What all this means is that there is a "core" calculation, plus some extra
tricks that may or may not come into play depending on the range of x. Figure 1
shows the mean time required to calculate Math.exp(x) for a range of
x values from -1 to +2.
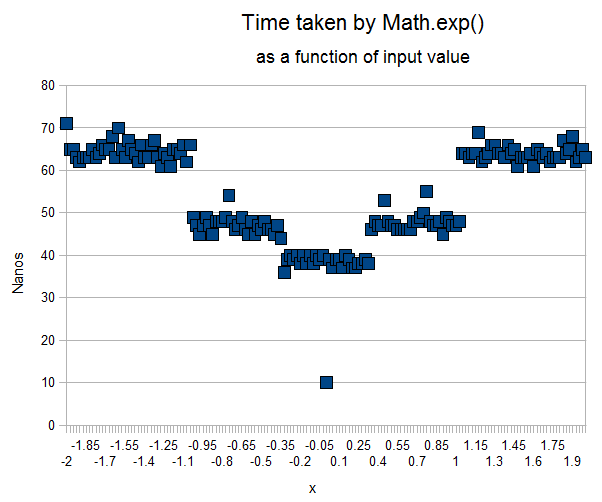
Figure 1: timing of Math.exp(x) as a function of the input value x.
As a guide, a floating point addition generally takes in the order of a nanosecond
on this machine.
The graph highlights firstly a range between around -0.035 and 0.035— in fact,
+/- 0.5 ln(2)— where only the "core" calculation needs to be made, taking
just under 40 nanoseconds. Then, there is
a range between around -1 and +1— in fact, +/- 1.5 ln(2)— where
x0 needs to be calcualted but where the calculation is relatively
simple (and the time rises to just under 50 nanoseconds).
Finally, for values outside this range, the calculation of x0
is slightly more complex and the overall time rises to over 60 nanoseconds.
The "blip" on the graph represents the special case of 0, where we know basically
without any effort (other than the method call and test) that the result is zero.
Although not shown on this graph, a further special "fast" case also concerns cases
where the magnitude of x is so large that it is known in advance that the
result would overflow or underflow the possible range of values of a double.
This occurs when x exceeds around 709, and in such cases the overall time
is around 20 nanoseconds.
Faster approximations to ex
For some applications, it is not crucial that the most
exact value of ex
possible be calculated: various less accurate approximations are often adequate.
A particularly useful approximation is based on the following
definition of ex:
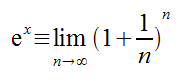
Or in other words, as we pick larger and larger values of n,
the calculation of (1 + 1/n)n will get closer and
closer to an accurate value of ex. In practice, useful
values of n will be powers of 2, because then, raising a number
to the power of n is equivalent to squaring (multiplying by itself)
a number of times. For example, the following example picking n = 256:
double exp(x) {
x = 1d + x / 256d;
x *= x; x *= x; x *= x; x *= x;
x *= x; x *= x; x *= x; x *= x;
return x;
}
is between 3 and 10 times faster than Math.exp() on
our i7 Q720 test system1.
Of course, this approximation is less accurate than Math.exp(). But
it is accurate to within 3 significant figures for input values
of x between +/1 -10. This is almost certainly accurate enough for various applications
(for example as the basis function in a neural network implementation). If it is not
accurate enough, then we can trade in time for extra accuracy simply by increasing n.
1. This range has to do with the quite complex nature of Intel and indeed other modern
processors. The function essentially compiles to a series of addition and multiplication
instructions. Where these can be interleaved with other instructions so that each instruction
is not dependent on an adjacent instruction, they can execute
at up to 1 instruction per clock cycle in the best case. In the worst case, they
take around 4 clock cycles per instruction.
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.