How Deflater works (ctd)
On the previous page, we took a brief overview of
dictionary compression in the
DEFLATE algorithm. After applying dictionary compression, the DEFLATE
algorithm applies a form of Huffman encoding, also known as
Huffman compression.
It is worth understanding Huffman encoding because one of the
options that the Deflater offers is to apply Huffman encoding only.
Huffman encoding
Huffman encoding is one of the most famous types of compression system. Even if it
is not used on its own, it is often used in conjunction with another compression scheme
(as indeed in the case here).
|
Huffman encoding works on a stream of bits. It takes an "alphabet"
of symbols (for example, the possible "symbols" could be the bytes 0-255,
but it could be some arbitrary range of numbers/values), and re-codes each symbol in
the alphabet as a sequence of bits, so that the sequence corresponding to each symbol
reflects the frequency of that symbol. The most frequently occurring symbol will
be represented by the shortest bit sequence, and with the length of each bit sequence
being roughly inversely proportional to its frequency.
Possible Huffman encodings can be worked out by creating a "Huffman tree" as follows:
- Start with a list of "nodes" consisting of the symbols and their
frequencies.
- Create a new node connecting the two least frequently occurring symbols.
- Label the branches with 0 and 1 (adopting some convention for whether
the branch to the least or most frequent symbol gets 0): in this example,
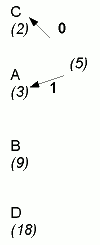
we'd connect A and C first.
- The newly created node gets a frequency which is the sum of the frequencies
of the two children: in this case it would be 2+3=5 (Fig 1).
- Repeat these steps until you end up with a single node which is the "root"
of the tree. So first we'd connect the newly created node with B (5 and 9 are
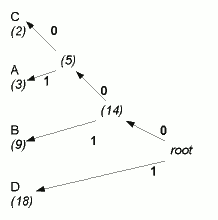
still the lowest frequencies), as in Fig 2; Fig 3 shows the completed tree.
- Start at the root and trace down the branches until you get to a "leaf" node
with one of the symbols: the sequence of 0s and 1s on the branches that you passed on the way
give the sequence for encoding that symbol. So in Fig 3, tracing from the root to the
symbol B gives a code of 01; C will have a code of 000; D, the most frequently
occurring symbol, will have a single-bit code, 1.
|
[Fig 1] | 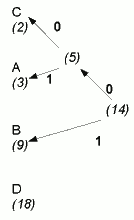
[Fig 2] |
[Fig 3]
|
When does Huffman coding perform well?
The idea of Huffman encoding is to assign each symbol a representation that
is inversely proportional to its frequency. But in reality, this is not usually
possible.
The problem is that the exact number of bits requred for a given symbol's length
to be inversely proportional to frequency could actually be a fractional number.
Huffman codes are only actually optimal when the probabilities of symbols are
negative powers of 2 (1/2, 1/4 etc): in other words, where there's one symbol occuring
around 50% of the time, then another around 25% of the time, etc.
However, if you do have data distributed in this way, you may be
able to take advantage of the Deflater's HUFFMAN_ONLY mode.
You may also be able to transform your data so that the distribution of
bytes is closer to the negative power of 2 relationship just described. On the next page,
I discuss a simple transformation that generally
improves text compression with the Deflater
by between 10 and 20%.
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.